25 al 29 de mayo
Les recuerdo que ya a mañana martes 26 de mayo, deben haber enviado el trabajo de la semana 13
No permito ( no doy permiso) para que me graben o tomen fotografías durante la clase virtual.
Les envío el link a su whatsapp cinco minutos antes de empezar clase ( 6:10 a.m), por Meet será la clase virtual.
Se hace necesario que aparezca su nombre completo y su grado, para poder identificarlo en la clase.
Se hace necesario que aparezca su nombre completo y su grado, para poder identificarlo en la clase.
Horario: Estoy en línea desde 6:15 a 12:15; y en clase virtual. Aunque 6° 1 en su horario habitual ha tenido clases los martes y miércoles a las 6:15, pueden ingresar los lunes a las 6:15 a.m para tener más tiempo de hacer los talleres.
Así mismo el grado 6° 2 tiene clase los lunes a las 6:15 a.m y pueden entrar el martes a las 6:15 a.m , también para que tengan suficiente tiempo para solucionar el taller de la semana.
Deben enviar el trabajo al correo mutispro3@gmail.com al finalizar la semana
Así mismo el grado 6° 2 tiene clase los lunes a las 6:15 a.m y pueden entrar el martes a las 6:15 a.m , también para que tengan suficiente tiempo para solucionar el taller de la semana.
Deben enviar el trabajo al correo mutispro3@gmail.com al finalizar la semana
INSTITUCIÓN EDUCATIVA JOSÉ CELESTINO MUTIS
GRADO: SEXTO
Área/ asignatura: Matemáticas
Duración: 4 horas semanales
Aprendizajes esperados:
Desarrollo del pensamiento numérico y resolución de algoritmos matemáticos identificando números pares, multiplicaciones con números naturales terminados en cero, descomposición de un número en factores primos y hallar el Máximo común Divisor.
Desarrollo del pensamiento numérico y resolución de algoritmos matemáticos identificando números pares, multiplicaciones con números naturales terminados en cero, descomposición de un número en factores primos y hallar el Máximo común Divisor.
Ámbitos conceptuales:
Números pares, multiplicaciones con números naturales terminados en cero, descomposición de un número en factores primos, Máximo común divisor).
Números pares, multiplicaciones con números naturales terminados en cero, descomposición de un número en factores primos, Máximo común divisor).
Metodología:
Videos, actividades variadas,encuentro virtual(CLASE), solución de taller aplicable al tema.
Videos, actividades variadas,encuentro virtual(CLASE), solución de taller aplicable al tema.
Actividades a desarrollar:
Explicación de la clase virtual, observación de videos referentes al tema, desarrollar juegos planteados en el link,solución del taller propuesto( en su cuaderno).
Explicación de la clase virtual, observación de videos referentes al tema, desarrollar juegos planteados en el link,solución del taller propuesto( en su cuaderno).
Recursos: Actividades a desarrollar, la web.
Bibliografía:
https://es.ixl.com/?partner=google&campaign=1934097723&adGroup=72390513244&gclid=EAIaIQobChMIxNC6pvTK6QIVkYHLAR29AwcEEAEYASAAEgJGIfD_BwE
https://www.smartick.es/blog/matematicas/multiplicaciones/multiplicar-por-un-numero-seguido-de-ceros/
https://es.ixl.com/?partner=google&campaign=1934097723&adGroup=72390513244&gclid=EAIaIQobChMIxNC6pvTK6QIVkYHLAR29AwcEEAEYASAAEgJGIfD_BwE
https://www.smartick.es/blog/matematicas/multiplicaciones/multiplicar-por-un-numero-seguido-de-ceros/
Esta parte de arriba no es necesario consignarla en tu cuaderno y los links son por si quieres ampliar tus conocimientos. Igualmente los contenidos sólo los consignas si crees que es necesario hacerlo para tu aprendizaje.
Horario: Estoy en línea desde 6:15 a 12:15; y en CLASE VIRTUAL en su horario de clase.
Lee los siguientes conceptos y mira los ejemplos para poder resolver el taller. También puedes apoyarte de los videos, si quieres( no tienes que hacer resumen de los videos y en tu cuaderno toma nota de lo que consideres necesario). Recuerda ingresar a la clase virtual.
Observa el video si consideras necesario verlo para ayudar a tu aprendizaje.
¿Qué es factorizar?
Factorizar es escribir un número como la multiplicación de otros números.
Por ejemplo, factorizamos el número 12.
12 = 3 x 4
12 = 2 x 6
12 = 1 x 12
Los tres casos son ejemplos de factorización.
En esta entrada vamos a explicar paso a paso cómo factorizar o descomponer un número en números primos.
Antes que nada, puedes consultar estas entradas donde explicábamos qué significa factorizar y qué es un número primo para refrescar la memoria.
Ahora ya estamos listos para empezar a descomponer un número en factores primos.
Vamos a factorizar el 12.
Paso 1
Escribimos el número que queremos factorizar seguido de una línea vertical.
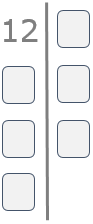
Paso 2
Buscamos el menor número primo divisor de 12. En nuestro ejemplo sería el 2.
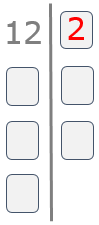
Paso 3
A continuación hacemos la división de 12 entre 2 y el resultado lo escribimos debajo del 12.
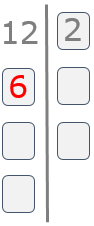
Paso 4
Repetimos el proceso. Buscamos el menor número primo divisor, en este caso, del 6. Como es un número par, de nuevo el 2 es el primo menor y lo escribimos al lado del 6.
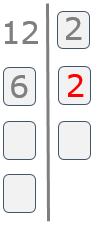
Paso 5
Volvemos a hacer la división de 6 entre 2 es igual a 3 y lo escribimos debajo del 6.

Paso 6
Volvemos a repetir el proceso. ¿Qué número primo es divisor de 3? El 3 mismo.
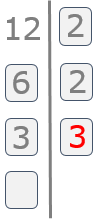
Paso 7
Hacemos la división. 3 entre 3 es igual a 1.

Paso 8
El proceso finaliza cuando hayamos llegado al 1. Nos quedamos con la segunda columna.
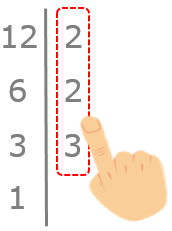
Y ya podemos expresar nuestro número como multiplicación de factores primos:
Siguiendo en orden estos pasos conseguimos descomponer un número en factores primos.
Todos los números se pueden expresar como multiplicación de factores primos.
Multiplicaciones por números naturales seguidos de ceros.
Para multiplicar por un número seguido de ceros primero se multiplica por el número sin los ceros, y después se añaden al resultado final todos los ceros que tenía el número.
Por ejemplo,
4000×6
Ignoramos los ceros del 4000 y multiplicamos los dos números,
4×6=24
Ahora añadimos los 3 ceros que tenía el número 4000
24000
Vamos a ver ahora otro ejemplo de cómo multiplicar un número seguido de ceros, pero esta vez con ceros en los dos números:
50×8000
Ahora, tanto el 50 como el 8000 tienen ceros. Los ignoramos de momento y multiplicamos los números,
5×8=40
Añadimos un cero del 50 y 3 ceros del 8000, en total añadimos 4 ceros,
400000
Y para terminar aquí dejo otro ejemplo:
2 x 3 = 6. Tenemos que añadir 2 ceros del 200 y 3 ceros del 3000. En total tenemos que añadir 5 ceros:
PUEDES JUGAR AQUÍ EN ESTE ENLACE SI QUIERES, DESCOMPONIENDO HASTA 80: https://www.smartick.es/exercise.html?resource=descomponer-numeros-hasta-80
CÓMO HALLAR EL MÁXIMO COMÚN DIVISOR (M.C. D.) POR DESCOMPOSICIÓN POLINÓMICA
Se busca un número que divida exactamente a todos los números dados para luego multiplicarlos.
Ejemplo 1: Hallar el Máximo Común Divisor ( M. C. D. ) de 36, 54, 90
SOLUCIÓN:
Descomponemos simultáneamente los números 36, 54 y 90, empezando por sacar mitad ya que terminan en cifra par, veamos:

M. C. D.( 36, 54, 90) = 2 x 3² = 2 x 9 = 18
Encontrar el M.C.D. de 24 y 36:
Solución: Buscamos todos los divisores de 24 y todos los divisores de 36, luego buscamos los que se repiten y seleccionamos el mayor de ellos ( ese será el máximo común divisor).
- Los divisores de 24 son: D 24={ 24, 12, 8, 6, 4, 3, 2, 1.}
- Los divisores de 36 son: D 36={18, 12, 9, 6, 4, 3, 2, 1.}
- Los divisores comunes de 24 y 36 son: D(24,36)= {12, 6, 4, 3, 2, 1.} El elemento mayor es 12.
- Por lo tanto, el máximo común divisor de 24 y 36 es 12.
Observa el video si consideras necesario verlo para ayudar a tu aprendizaje.
Taller semana 14 ( Debes trabajar diario un punto, ya que te permite entrar uno por día)
1. Vaya al enlace y juegue acerca de factorizar , luego escribe algunos en tu cuaderno.
2. Identifica los números pares e impares en este enlace, debes jugarlo aquí y escribir algunos en tu cuaderno
3. Vaya al enlace y juegue buscando los divisores de un número dado, copia algunos en tu cuaderno. En este enlace:
4.Multiplica por números que terminan en cero. Ve al siguiente enlace, juega y escribe en tu cuaderno algunos de ellos.
5. Descomponer en factores primos los siguientes números y escriba la respuesta en cada caso: ( recuerde trazar la línea para descomponer)
a) 120 b) 81 c) 50 d) 27 e) 75 f) 49
6. Hallar el M. C. D ( Máximo Común Divisor). Para ello ve al siguiente enlace, observa, juega y realiza algunos en tu cuaderno con el procedimiento.
Si usted considera que no necesita solucionar todos los ejercicios propuestos en este taller, porque ya has aprendido bien el tema, pues no los haces todos.
No tienen que copiar los conceptos en el cuaderno.



No hay comentarios:
Publicar un comentario