Aprendizajes esperados:
Desarrollo del pensamiento numérico y resolución de algoritmos matemáticos identificando números pares, multiplicaciones con números naturales terminados en cero, descomposición de un número en factores primos y hallar el Máximo común Divisor.
Ámbitos conceptuales:
Descomposición de un número en factores primos, mínimo común múltiplo, Máximo común divisor).
Descomposición de un número en factores primos, mínimo común múltiplo, Máximo común divisor).
¿Qué es factorizar?
Factorizar es escribir un número como la multiplicación de otros números.
Por ejemplo, factorizamos el número 12.
12 = 3 x 4
12 = 2 x 6
12 = 1 x 12
Los tres casos son ejemplos de factorización.
En esta entrada vamos a explicar paso a paso cómo factorizar o descomponer un número en números primos.
Vamos a factorizar el 12.
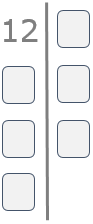
Paso 1
Escribimos el número que queremos factorizar seguido de una línea vertical.
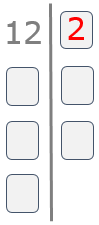
Paso 2
Buscamos el menor número primo divisor de 12. En nuestro ejemplo sería el 2.
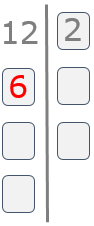
Paso 3
A continuación hacemos la división de 12 entre 2 y el resultado lo escribimos debajo del 12.
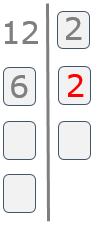
Paso 4
Repetimos el proceso. Buscamos el menor número primo divisor, en este caso, del 6. Como es un número par, de nuevo el 2 es el primo menor y lo escribimos al lado del 6.
Paso 5
Volvemos a hacer la división de 6 entre 2 es igual a 3 y lo escribimos debajo del 6.
Paso 6
Volvemos a repetir el proceso. ¿Qué número primo es divisor de 3? El 3 mismo.
Paso 7
Hacemos la división. 3 entre 3 es igual a 1.
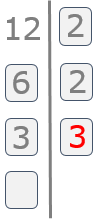
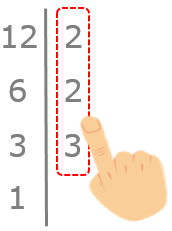
Paso 8
El proceso finaliza cuando hayamos llegado al 1. Nos quedamos con la segunda columna.
Y ya podemos expresar nuestro número como multiplicación de factores primos:
Siguiendo en orden estos pasos conseguimos descomponer un número en factores primos.
Todos los números se pueden expresar como multiplicación de factores primos.
Tema: m.c.m. y M.C.D.
Objetivo: Calcular el mínimo común múltiplo y el máximo común divisor de dos o más números usando los métodos de descomposición en factores primos y por búsqueda de múltiplos o divisores.DBA: Identifica los múltiplos y divisores comunes entre números naturales para resolver situaciones problemáticas.
Objetivos:
- Conocer y calcular el mcm y el MCD por descomposición factorial de los números.
- Comprender y aplicar el mcm por los múltiplos comunes de los números.
- Comprender y aplicar el MCD por los divisores comunes de los números.
VER LOS VIDEOS:
Mínimo común múltiplo de las dos formas
Máximo común Divisor de las dos formas
Cómo descomponer un número en factores primos?
Mínimo común múltiplo (m.c.m)
El (m.c.m.) nos permite conocer cuál es el número más pequeño que es múltiplo de un determinado conjunto de números. Existen dos formas para hallar el m.c.m:
Ver video clic
Primera forma:
Para hallar el mínimo común múltiplo de dos o más números debemos de descomponer el número en factores primos. Por ejemplo:
Hallar el mínimo común múltiplo (m.c.m) de 72 y 50:
Se descomponen simultáneamente los números 72 y 50:
El m.c.m es la multiplicación de los factores primos que resultaron:
m.c.m (72,50) = 2 x 2 x 2 x 3 x 3 x 5 x 5
O sea: 8x 9x25
72x25=1800 entonces el m.c.m (72,50)=1.800
Segunda forma:
Buscando los múltiplos de los números dados , luego escogemos los que son comunes y de allí buscamos el menor de los comunes( ese será el m.c.m)
Los múltiplos de un número son los que obtienes cuando lo multiplicas por otros números.
Ejemplo uno: Hallar el m.c.m. de 2 y 3
Debo saberme la tabla del 2 y del 3, así:
Vamos a ver los múltiplos comunes de 2 y de 3 ( o sea los que se repiten)
Escogemos el menor de ellos que es 6
Entonces m.c.m ( 2, 3) = 6
2. Ejemplo: Averiguar el m.c.m. de Sacar el m.c.m. de 20 y 10:
20 = 20, 40, 60, 80.....
10= 10, 20, 30, 40....
20 es el múltiplo menor que es común a ambos números. Entonces: m.c.m(20,10) = 20
Máximo común Divisor ( M.C.D)
El máximo común divisor de dos o más números naturales (enteros positivos) es, como su nombre indica, el mayor de los divisores comunes a dichos números.
Hay dos formas para hallar el Máximo Común Divisor:
Primera forma: Buscamos todos los divisores de los números dados y señalamos los que son comunes, luego escogemos el mayor de ellos.
Ejemplo:
Hallar el máximo Común Divisor de 6,12,18
Los divisores de 12 son ⇒ 1, 2, 3, 4, 6, 12
Los divisores de 18 son ⇒ 1, 2, 3, 6, 9, 18
Los divisores comunes de 6, 12 y 18 son ⇒ 1, 2, 3, 6
Como el mayor es 6, el M.C.D. (6 , 12 , 18) = 6
Segunda forma:
También existe otro método que es descomponiendo en factores primos, por descomposición simultánea:
M.C.D.( 36,54,90) = 2x3x3: 18
Observe, que el 2, 3, 5 los dejé así porque los tres números no se podían dividir a la vez por el mismo número; entonces hasta ahí llegamos y quedan sin descomponer.
Taller 19
Tema: Mínimo común múltiplo(m.c.m) y Máximo Común Divisor(M.C.D)
1. Hallar el m.c.m de 18, 24 y 36 de la forma larga y corta ( las dos formas explicadas en clase)
2. Hallar el M.C.D. de 20, 30 y 40 de la forma larga y corta ( Las dos formas explicadas en clase)
VER ESTOS VIDEOS QUE TE PUEDEN AYUDAR A REFORZAR EL TEMA. Sólo hacer clic cobre el link azul.
No hay comentarios:
Publicar un comentario