Objetivos:
- Comparar fracciones con igual y con diferente denominador.
- Identificar las clases de fraccionarios, estableciendo comparaciones entre ellos.
- Hallar fracciones equivalentes a otras fracciones dadas, a través de la simplificación y amplificación de fracciones.
- Ubicar números fraccionarios en la recta numérica.
Aprendizajes esperados:
Desarrollo del pensamiento numérico y resolución de algoritmos matemáticos representando números fraccionarios en la recta numérica, comparación, búsqueda de equivalencias, amplificación y simplificación, clasificación de los números fraccionarios.
Desarrollo del pensamiento numérico y resolución de algoritmos matemáticos representando números fraccionarios en la recta numérica, comparación, búsqueda de equivalencias, amplificación y simplificación, clasificación de los números fraccionarios.
Ámbitos conceptuales:
Números fraccionarios, representación en la recta numérica de números fraccionarios, comparación de fracciones de igual y diferente denominador, fracciones equivalentes, clases de fracciones.
Números fraccionarios, representación en la recta numérica de números fraccionarios, comparación de fracciones de igual y diferente denominador, fracciones equivalentes, clases de fracciones.
Metodología:
Videos, actividades variadas, encuentro presencial(CLASE), solución de taller aplicable al tema de fracciones.
Videos, actividades variadas, encuentro presencial(CLASE), solución de taller aplicable al tema de fracciones.
Actividades a desarrollar:
Explicación de la clase virtual, observación de videos referentes al tema, representación en la recta numérica de fracciones, comparación de fracciones, clasificación de las fracciones, solución del taller propuesto( en su cuaderno).
Explicación de la clase virtual, observación de videos referentes al tema, representación en la recta numérica de fracciones, comparación de fracciones, clasificación de las fracciones, solución del taller propuesto( en su cuaderno).
Recursos: Actividades a desarrollar, la web.
Bibliografía:
https://www.elabueloeduca.com/aprender/matematicas/fracciones/fracciones.html
https://www.unprofesor.com/matematicas/como-representar-fracciones-299.html
https://www.webcolegios.com/file/ac5dbf.pdf
https://www.elabueloeduca.com/aprender/matematicas/fracciones/fracciones.html
https://www.unprofesor.com/matematicas/como-representar-fracciones-299.html
https://www.webcolegios.com/file/ac5dbf.pdf
Observe los siguientes videos:
CÓMO LEER FRACCIONES?
CÓMO REPRESENTAR UN NÚMERO FRACCIONARIO EN LA RECTA NUMÉRICA?
clic
CLASES DE NÚMERO FRACCIONARIOS
CLASES DE NÚMERO FRACCIONARIOS
CÓMO AMPLIFICAR UN NÚMERO FRACCIONARIO?
Representar fracciones en la recta numérica
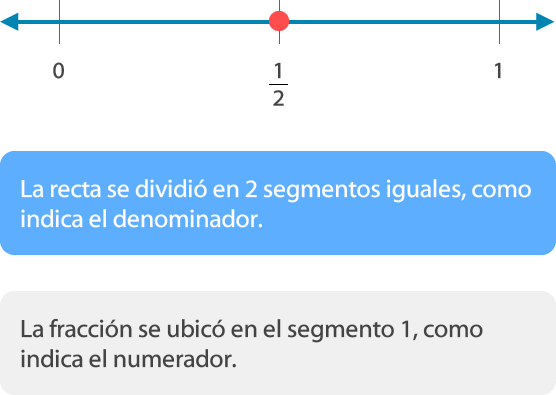
Para ubicar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la facción según indica el numerador.
Ejemplo de fracciones unitarias (con numerador 1) en la recta numérica:
a. Ubicar la fracción
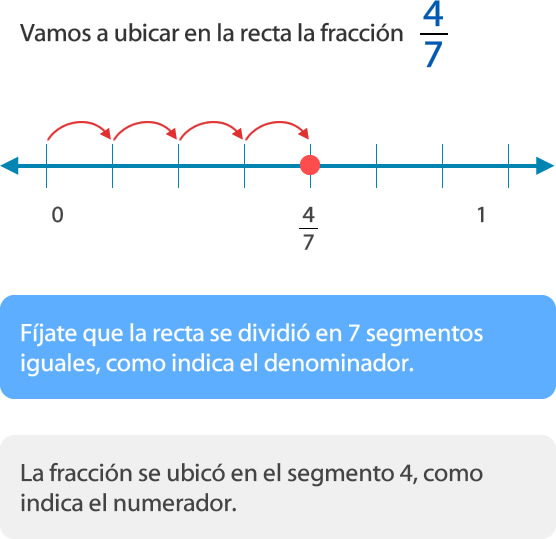
b. Ubicar la fracción

c.
Clasificación de las Fracciones
Las fracciones se pueden clasificar de distintas formas; en la siguiente tabla se muestran las características de las más importantes.
| Tipo | Características | Ejemplos |
|---|---|---|
| Propia | El numerador es menor que el denominador. | 1/2, 7/9 |
| Impropia | El numerador es mayor que el denominador. | 4/3, 5/2 |
| Homogéneas | Tienen el mismo denominador. | 2/5, 4/5 |
| Heterogéneas | Tienen distinto denominador. | 3/7, 2/8 |
| Entera | El numerador es igual al denominador; representa un entero. | 6/6 = 1 |
| Equivalentes | Cuando tienen el mismo valor. Dos fracciones son equivalentes si son iguales sus productos cruzados. | 2/3 y 4/6 2x6=3x4 |
Fracción igual a la unidad:
son aquellas fracciones en las que el numerador y el denominador valen lo mismo por lo que su resultado será igual a la unidad (9/9 = 1). Ejemplos:
2/2 = 1
3/3 = 1
10/10 = 1
13/13 = 1
Números mixtos:
El número mixto o fracción mixta está compuesto de una parte entera y otra fraccionaria.
Ejemplo:
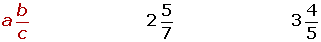













No hay comentarios:
Publicar un comentario